Hypothesis Testing

Re# Hypothesis Testing### Description:

• 

Using Confidence interval:

• To test claims about a population mean $\mu$, we construct a confidence interval (a, b).
  • Claim: $\mu ={\mu }_0$ Do not reject test-claim if ${\mu }_0\in (a,b)$, reject otherwise.
  • Claim: $\mu <{\mu }_0$. Do not reject test-claim if $b<{\mu }_0$, reject otherwise.
  • Claim: $\mu >{\mu }_0$. Do not reject test-claim if ${\mu }_0<a$ , reject otherwise.

Null Hypothesis and Alternative Hypothesis

One-tailed vs two-tailed:

1. $H_0:\mu \ge {\mu }_0,H_a:\mu <{\mu }_0$, lower one-tailed
2. $H_0:\mu \le {\mu }_0,H_a:\mu >{\mu }_0$, upper one-tailed
3. $H_1:\mu ={\mu }_0,H_a:\mu \ne {\mu }_0$, two-tailed

Test statistic:

• Used to compare against another critical value to evaluate hypothesis
• All test statistic value must lie outside of Confidence interval $1-\alpha$, to be rejected
• For p-value:
  • Use Normal distribution, $ts=\frac{\bar{x}-{\mu }_0}{{\sigma }_x}$
  • for two-tailed, $p$-value is divided by 2
• For t-value: t test
• For Proportion:
  • Use Population Proportion
  • $ts=\frac{\bar{p}-p_0}{\sqrt{\frac{p_0.(1-p_0)}{n}}}$
• For Difference random variable of 2 variables:
  • For known $\sigma$
    • Because ${\bar{x}}_1-{\bar{x}}_2\sim N(D_0,\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}})$
    • $ts=\frac{{\bar{x}}_1-{\bar{x}}_2-D_0}{\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}}}$
      • $D_0={\mu }_1-{\mu }_2$
  • For unknown $\sigma$
    • t test use t-distribution with degree of freedom
    • $ts=\frac{{\bar{x}}_1-{\bar{x}}_2-D_0}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$
• For Match samples
  • $ts=\frac{\bar{d}-{\mu }_d}{s_d/\sqrt{n}}$ with $n-1$ deg
• For [[Population Proportion#inteference-about-p_1-p_2|Inteference about $p_1-p_2$]]:
  • Under assumption, $H_0:p_1-p_2=0,p_1=p_2=p$
  • ${\sigma }_{{\bar{p}}_1-{\bar{p}}_2}=\sqrt{\frac{p(1-p)}{n_1}+\frac{p(1-p)}{n_2}}=\sqrt{p(1-p)(\frac{1}{n_1}+\frac{1}{n_2})}$
  • With $p$ unknown, we can estimate $p$ by pooled estimator:
    • $\bar{p}=\frac{n_1{\bar{p}}_1+n_2{\bar{p}}_2}{n_1+n_2}$
  • $ts=z=\frac{{\bar{p}}_1-{\bar{p}}_2}{\sqrt{\bar{p}\bar{q}(\frac{1}{n_1}+\frac{1}{n_2})}}$

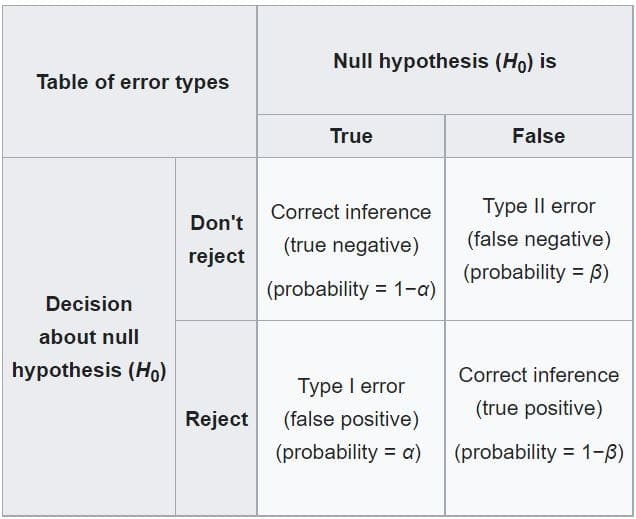
Type 1 Error vs Type 2 Error

Level of significance:

• Same as probability of making a Type 1 Error
• When the null hypothesis is true as an equality
• If the cost of making a Type I error is high, small values of α are preferred.
  • Like medication, must have small LoS
• If the cost of making a Type I error is not too high, larger values of α are typically used.
  • it is sometimes ok to make mistake, but low chance

---